7 Ergebnisse

Das tidyverse wird geladen und die zwei Basispakete kableExtra sowie scales. Dann werden aus _common.R ein paar Einstellungen geladen und dann die Datensätze für die Inhaltsanalyse un die Befragung.

7.1 Wofür welcher Datensatz?

Für die meisten Auswertungen wird der Datensatz der Inhaltsanalyse schon reichen. Sie können damit beschreiben, in welchem Umfang welche Nachrichtenfaktoren vorkommen und welche Ausprägungen sie haben. Sie können auch testen, welche Nachrichtenfaktoren mit der journalistischen Beachtung (Platzierung und Umfang der Beiträge) in welchem Masse zusammenhängen (Kreuztabellen und Korrelationen). Sie können auch analysieren, wie die Nachrichtenfaktoren untereinander zusammenhängen und inwiefern sie in der Summe die journalistische Beachtung besser erklären als einzelne Nachrichtenfaktoren (Additivitätshypothese). Sie können auch untersuchen, ob bestimmte NF in Mediengruppen häufiger vorkommen und stärkere Durchschnittsintensitäten haben als in anderen. Mit den Daten der Inhaltsanalyse lassen sich also viele Hypothesen schon aufklären.

Was allein mit dem Datensatz der Inhaltsanalyse nicht geht, ist die Bedeutung der NF für die Aufmerksamkeit bzw. Erinnerung an Meldungen durch die Rezipienten. Dafür braucht es die Ergänzung durch die Erkenntnisse aus der Befragung. Darum werden die Nennungen von Meldungen an den Inhaltsanalysedatensatz angefügt, also die Datensätze fusioniert. Dann können Sie das, was Sie mit der journalistischen Beachtung gemacht haben, für die Nennungen der Meldungen wiederholen und vergleichen, welche NF für die journalistische Beachtung eine andere Rolle spielen als für die Rezipienten. Wenn Sie aus der Befragung noch Informationen haben, für wie wichtig oder interessant die Befragten die von ihnen genannten Meldungen finden oder worüber sich die Befragten mit anderen unterhalten haben, dann können Sie feststellen, welche NF mehr auf das Interesse abzielen und welche eher als wichtig empfunden werden und welche mitbestimmen, worüber man sich so unterhält (was also Gesprächswert hat). Mit dem fusionierten Datensatz, bei dem die Inhaltsanalyse primär ist und die Nennungen der Befragten angefügt wurden, können die meisten Hypothesen überprüft werden, da hier zum reinen IA-Datensatz noch die Informationen der Befragten hinzukommen.

Der Befragungsdatensatz alleine enthält nicht allzu viele Informationen. Die quasiexperimentellen Fragen, was für Schlagzeilen die Leute wie spannend finden, sind in der Regel nicht sehr ergiebig, weil sie eben nicht sehr valide sind (zu abstrakt und artifiziell). Die Befragung entfaltet ihren eigentlichen Wert erst mit der Datenfusion wie im vorherigen Abschnitt beschrieben. Allerdings haben Sie auch Daten über die Befragten, die dabei helfen können, die Befragten in Gruppen einzuteilen und dann zu schauen, welche Nachrichtenfaktoren bei diese Gruppen eine besondere Bedeutung haben. Dazu braucht es die Datenfusion der NF aus der Inhaltsanalyse an den Befragungsdatensatz. Dann haben sie für jeden Befragten, die durchschnittlichen Intensitäten (von 0 bis irgendwas) der Nachrichtenfaktoren, wie sie in den Meldungen vorkommen, die die Befragten genannt haben. Sie könnten also zB feststellen, ob ältere Befragte eher Meldungen mit anderen NF nennen als die jüngeren Befragte. Das wird vor allem spannend, wenn Sie die Nuter:innen von Medien unterteilen und schauen, ob vielleicht Promistatus oder individueller Schaden bei Leser:innen von Boulevard- oder reinen Onlinemedien besonders hoch im Kurs sind und bei SRF- oder NZZ-Nutzer:innen eine geringere Rolle spielen. Sie könnten sogar eine Faktorenanalyse der NF der Befragten durchführen und so herausfinden, welche Kombinationen von NF bei den Befragten stärker zusammenhängen. Und sie könnten explorativ eine Clusteranalyse durchführen und Gruppen von Befragten Bilden, die deutlich machen, dass es unterscheidbare Nutzer:innengruppen bei der Rezeption von Nachrichten gibt. Sie müssen nicht, aber Sie können das machen.

Manche AGs werden fast nur mit dem Datensatz arbeiten, der aus der Datenfusion von IA + Befragung entstanden ist (mit der IA alleine, werden viele Hypothesen ungeklärt bleiben, was natürlich nicht gut wäre). Da es Gruppen gibt, die Hypothesen darüber haben, wie sich die Bedeutung der NF zwischen Nutzer:innengruppen unterscheiden, brauchen die auch den Datensatz aus der Fusion Befragung + IA. Da ist die Fusion allerdings aufwendiger, fehleranfälliger und im Ergebnis mühsamer. Für das Zeitmanagement sollten alle AGs schon früh die vorbereinigten Daten aus der Befragung und der Inhaltsanalyse haben, um starten zu können. Wenn die Datenfusion IA + Befragung funktioniert hat und fertig ist, sollte die zur Verfügung gestellt werden. Als letztes sollten die fusionierten Daten aus Befragung + IA ausgegeben werden. Aus der stufenweisen Verteilung der Daten folgt, dass Datenaufbereitungen wiederholt werden müssen, also zB die Umkodierungen (mutate) und Labelei nochmals durchlaufen muss, die für die unfusionierten IA-Daten gemacht wurden, wenn die fusionierten Daten kommen. Das sollte allerdings kein Probleme sein, da diese Transformationen in R- oder Rmd-Dateien gespeichert sind und einfach nochmal durchlaufen müssen.

7.2 Stichprobenbeschreibung

Hier werden die Ergebnisse vor allem in Tabellenform präsentiert (Für ein Beispiel eines Verweises auf eine Tabelle siehe Tabelle @ref(tab:Mehrfachantworten)). Im Unikontext sind Grafiken und Diagramme eher dann angebracht, wenn Tabellen weniger Informationen bereitstellen würden oder so unübersichtlich würden, dass man sie kaum noch lesen kann. Das ist im normalen Studium selten der Fall. Schöne Diagramme können eine Arbeit optisch aufwerten aber meistens nicht inhaltlich. Wenn Grafiken für die Ergebnisdarstellung genutzt werden, sollten immer die differenzierteren Tabellen im Anhang aufgeführt werden.

7.3 Häufigkeitstabelle mit Mehrfachantworten

Gerade in der Befragung haben Sie mehrere Fragen mit der Möglichkeit zu Mehrfachantworten. Das führt dann immer zu einem ganzen Set von Variablen, die immer eine 1 für “angekreuzt” enthalten und 0 für “nicht angekreuzt”. Wenn von solch einer Frage mit der Möglichkeit zu Mehrfachanworten eine Häufigkeitsauszählung gemacht werden soll, dann muss man aufpassen, worauf prozentuiert wird: auf die Anzahl der abgegebenen Antworten oder auf die Anzahl Fälle (im Fall, Befragte).

# mit dem Paket "ufs" recht einfach 

DATEN_BF |> 
  select(NACHRICHT_TITEL1:NACHRICHT_TITEL6, M112_20, M112_21, M112_23) |> # hiermit die Variablen auswählen, die zu den Ausprägungen werden
  sjlabelled::label_to_colnames() |>  # hier werden die Label der Variablen zu den Zeilennamen
  ufs::multiResponse() |> # produziert die Tabelle für die Merhfachantworten
  rename("Medium" = "Option", # Hier werden die Spalten umbenannt
         "n" = "Frequency", 
         "Prozent Antworten" = "Percentage of responses", 
         "Prozent Fälle" = "Percentage of (203) cases" # hier das "#" wegmachen, wenn Sie die richtige Anzahl statt "(203) cases" eingetragen haben
        ) |>
  mutate(across(3:4, ~scales::percent(.x/100,accuracy = 2))) |> 
  kableExtra::kable(caption = "Mediennuztung der Befragten",
        booktabs = T, 
        align = c('l', 'r', 'r', 'r', 'r'), # wenn ab der zweiten Spalte alles rechtsbündig, dann geht auch rep("r", NCOL(employ_frq)-1)
        linesep = "") |> 
   kableExtra::footnote(general = "Lesebeispiel: 34% der Befragten haben die NZZ genannt. Die NZZ macht 12% aller 544 Mediennennungen aus.",
            general_title = "", # damit Kable unten nicht "Note" schreibt
           threeparttable = T # damit längere Fussnoten umgebrochen werden
           ) |> 
  kableExtra::kable_styling()
## Registered S3 method overwritten by 'webshot':
##   method        from    
##   print.webshot webshot2

Mediennuztung der Befragten
Medium	n	Prozent Antworten	Prozent Fälle
NZZ	67	12%	34%
TA	57	10%	28%
20 Minuten	107	20%	52%
Blick	43	8%	22%
Watson	32	6%	16%
SRF News	79	14%	38%
Social Media	66	12%	32%
Google News	17	4%	8%
anderes	76	14%	38%
Total	544	100%	268%
Lesebeispiel: 34% der Befragten haben die NZZ genannt. Die NZZ macht 12% aller 544 Mediennennungen aus.

7.4 Vorkommen der NF

Es können am Anfang die wichtigsten Variablen für die Stichrpobenbeschreibung auch als einfache Häufigkeitsauszählungen dargestellt werden. Häufigkeitsauszählungen stellen die komplette Information einer Variablen dar, da jede mögliche Ausprägung wiedergegeben wird und ihre Anzahl im Datensatz. Das sind relativ viele Inoformationen. Wenn man das für mehrere Variablen macht, wird das viel Aufwand.

### Wenn Sie die Label bei der Datenaufbereitung schon vergeben haben, müssen Sie das hier natürlich nicht wiederholen

KNTR_frq <- DATEN_IA |> # baue eine Häufigkeitstabelle
  select(KNTR) |> # nur KNTR auswählen
  sjlabelled::as_label() |>  # die Label verwenden
  tidycomm::tab_frequencies(KNTR) |> # eine Häufigkeitstabelle erstellt wird
  janitor::adorn_totals() |> # mit dieser Zeile können Sie eine Gesamtzeile unter Ihrer Tabelle einfügen
  mutate(Prozent = paste0(as.character(round(percent * 100, 0)),"%")) |> # Wenn Sie Prozentangaben mit %-Zeichen möchten
  select(1, n, Prozent) # hier nehmen wir von den Daten nur die erste Spalte 1 und die Fallzahl n und die Prozent

KNTR_frq |> 
 kableExtra::kable(caption = "Kontroverse",
        booktabs = T, 
        align = c('l', rep('r',2)), # die 10 steht dafür, dass 10 weitere Spalten alle rechtsbündig sind bzw. wären
        linesep = "", # ohne diese Zeile, macht knitr alle 5 Zeilen einen kleinen Abstand, der oft kaum Sinn macht
        col.names = c("Kontroverse", "Häufigkeit", "Prozent"), # Damit können die Überschriften neu gemacht werden
        ) |>  # noch mehr Anpassungsmöglichkeiten für kable finden Sie bei google: r kable 
  kableExtra::footnote(general = "Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.",
            general_title = "", # damit Kable unten nicht "Note" schreibt
           threeparttable = T # damit längere Fussnoten umgebrochen werden
           ) |> 
  kableExtra::kable_styling()

Kontroverse
Kontroverse	Häufigkeit	Prozent
keine	297	60%
gering	145	29%
stark	57	11%
Total	499	100%
Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.


rm(KNTR_frq) # Wird nicht mehr gebraucht und kann daher removed werden.

Textbeispiel: In 60 Prozent der Onlinebeiträge kam der Nachrichtenfaktor “Kontroverse” nicht vor. In knapp einem Drittel der Artikel wurde eine “geringe” Kontroverse beschrieben. In 57 Artikeln von 499 wurde eine starke Kontroverse thematisiert (11%).

7.5 Vergleiche des Vorkommens

Da das einzelne Vorkommen von Nachrichtenfaktoren im Grunde nichts über ihre Bedeutung sagt, sollten das Vorkommen der NF verglichen werden. Da die Nachrichtenfaktoren aber in der Regel mit unterschiedlichen Ausprägungen gemessen wurden, müssen sie erstmal auf einen gemeinsamen Standard gebracht werden. Das geht zum Beispiel indem man sie in Dummyvariablen umwandelt, also immer dann eine 0 setzt, wenn ein NF nicht vorkam (Wert 0 im Datensatz) und 1, wenn er grösser war als 0, also 1, 2, 3 usw. Mit solchen Dummyvariablen kann man ganz gut rechnen. So ist der Mittelwert einer Dummyvariable gleich dem Proporz der 1er (Summe der 1 = Vorkommen der 1 dividiert durch die Anzahl). Wenn man das mal 100 rechnet, dann hat man die Prozentwerte.

DATEN_IA <- DATEN_IA |> 
  sjlabelled::var_labels(PERS = "Personalisierung", KNTR = "Kontroverse", SCHAD = "Schaden", NAEHE = "Nähe")

DATEN_IA |> 
  select(PERS, KNTR, SCHAD, NAEHE) |> # Auswahl Ihrer NFs
  sjlabelled::label_to_colnames() |> 
  mutate(across(everything(), ~if_else(.x > 0, 1, 0))) |> # Hier alle gleich behandeln, indem alles was grösser als 0 zu 1 wird und alles andere zu 0 (Dummykodierung 0/1)
  summarise(across(everything(), ~round(mean(.x, na.rm = TRUE),2)*100)) |> # Mittelwert von 0/1-Dummyvariablen * 100 ist Prozent, gerundet mit 0 Nachkommastellen
  pivot_longer(cols = (Personalisierung:Nähe), names_to = "NFs", values_to = "Prozent") |>  # Die Tabelle muss noch ins Längsformat gebracht werden für das Balkendiagramm
  ggplot(aes(NFs, Prozent)) + # ACHTUNG bei ggplot für die Diagramme wird das + verwendet und nicht |> 
  geom_col(fill = Farben[1]) + # Die Farbpalette können Sie in _common.R festlegen wie Sie wollen
  geom_text(aes(label = paste0(format(Prozent), "%")), vjust = -.4) +
  theme_minimal() +
    xlab("Nachrichtenfaktoren")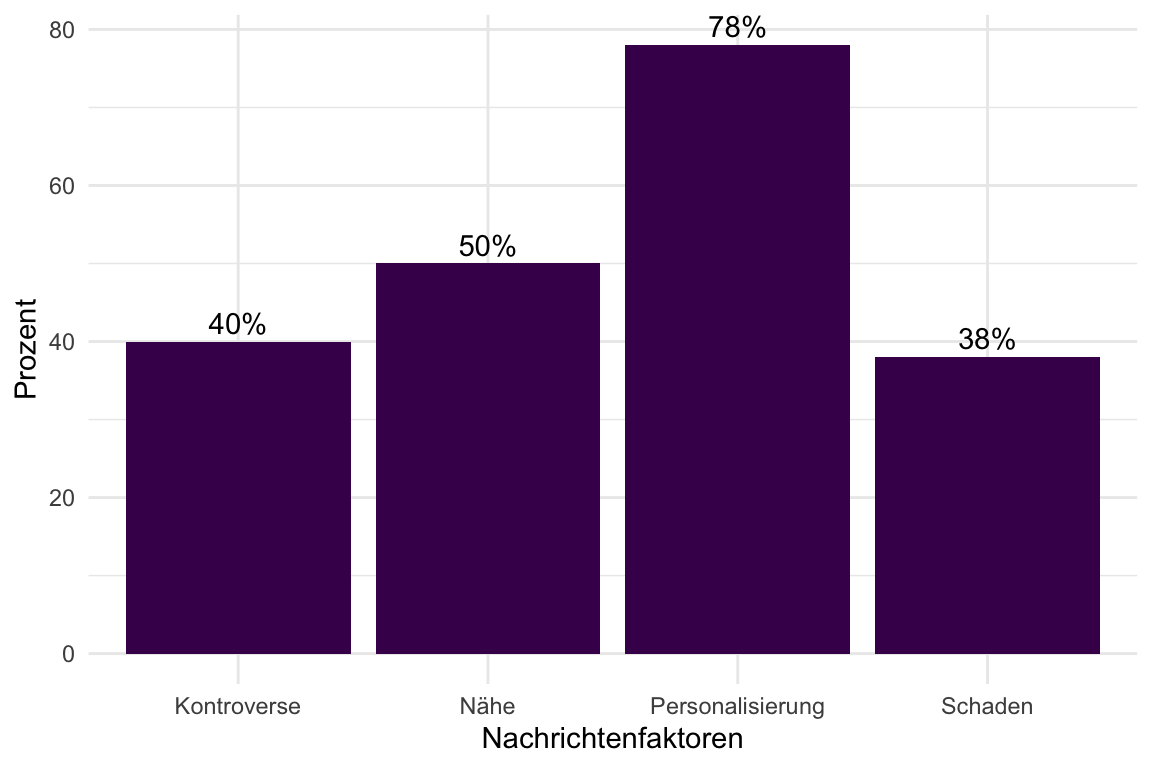

Textbeispiel: Personalisierung kam in 78 Prozent der Artikel vor. Das bedeutet, dass Personalisierung für die Berichterstattung ein wichtiger Nachrichtenfaktor ist. Ohne Personen geht es offenbar nicht. Die “Nähe” der berichteten Ereignisse ist in 50 Prozent der Artikel gegeben. Das deutet darauf hin, dass die Belange von besonderer Bedeutung sind, die eine höhere Betroffenheit für die Schweizer Bevölkerung haben, weil sie in ihrere Nähe passieren. Medien berichten vor allem auch über Kontroversen oder kontroverse Themen. In der Stichprobe waren 40 Prozent der Artikel von Kontroversen geprägt. 38 Prozent der Artikel thematisierten einen “Schaden”. Das bedeutet einerseits, dass 62% der Artikel keinen Schaden thematisiert haben, also dennoch wichtig genug waren. Andererseits bedeutet das, dass Eregnisse mit der Thematisierung von Schäden häufig in den Medien aufgegriffen werden. Um die Bedeutung der NFs im Vergleich beurteilen zu können, muss noch untersucht werden, ob sie alleine stark genug sind, um einen hohen Nachrichtenwert zu begründen oder erst durch das Zusammenspiel mit anderen Nachrichtenfaktoren eine Rolle spielen.

7.6 Bedeutung der Nachrichtenfaktoren für die journalistische Selektion

DATEN_IA <- DATEN_IA |> 
  mutate(Nenn_Gr = sjmisc::rec(Nenn_Gesamt, rec = "1:3 = 1; 4:16 = 2; 17:100 = 3")) |> 
  sjlabelled::set_labels(Nenn_Gr, labels = (c("selten" = 1, "mittel" = 2, "häufig" = 3)))

# DATEN_IA |> frq(Nenn_Gr) Immer mal schnell checken mit frq, aber nie in den Output!

SCHAD_Nenn_KREUZ <- DATEN_IA |> 
  sjlabelled::as_label() |> 
  tidycomm::crosstab(SCHAD, Nenn_Gr, add_total = TRUE, percentages = TRUE, chi_square = TRUE) |> # Chi^2 finden sie in der Console und können es in die Fussnote kopieren
  select(-any_of("<NA>")) |> 
  janitor::adorn_totals() |> # Wieder die Gesamtzeile
  mutate(across(c(-1), ~paste0(as.character(round(.x * 100, 0)),"%")))  # Wenn Sie Prozentangaben mit %-Zeichen möchten

SCHAD_Nenn_KREUZ |> # Jetzt wird die Tabele noch hübsch gemacht
    kableExtra::kable(caption = "Kreuztabelle für Schaden und Rezipienten-Nennungen", # ne Überschrift
        booktabs = T, # das sorgt für gute Bücherqualitätstabellen
        align = c('l', rep('r', NCOL(SCHAD_Nenn_KREUZ)-1)), # wenn ab der zweiten Spalte alles rechtsbündig, dann geht auch rep("r", NCOL(employ_frq)-1)
        linesep = "", # ohne diese Zeile, macht knitr alle 5 Zeilen einen kleinen Abstand, der oft kaum Sinn macht
       col.names = c("Nennungen", "keiner", "gering", "gross", "Gesamt"), # Damit können die Überschriften neu gemacht werden
        ) |>  # noch mehr Anpassungsmöglichkeiten für kable finden Sie bei google: r kable 
      kableExtra::kable_styling() |>  # hier können Sie stylen, aber bleiben Sie seriös :-)
  kableExtra::footnote(general = "Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.",
            general_title = "", # damit Kable unten nicht "Note" schreibt
            threeparttable = T # damit längere Fussnoten umgebrochen werden
           ) |> kableExtra::add_header_above(c("", "Schaden" = 3, "")) |> 
  kableExtra::row_spec(4, bold = TRUE)

Kreuztabelle für Schaden und Rezipienten-Nennungen
	Schaden
Nennungen	keiner	gering	gross	Gesamt
selten	14%	5%	7%	11%
mittel	27%	22%	46%	30%
häufig	59%	73%	46%	59%
Total	100%	100%	100%	100%
Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.

Textbeispiel: Wenn Onlinebeiträge keinen Schaden aufweisen, werden sie am häufigsten von den Rezipienten nur selten genannt (14%). Nennungen mittlerer Häufigkeit korrespondieren am häufigsten mit grossem Schaden (46%). Die häufigsten Nennungen kommen dann zustande, wenn Meldungen einen geringen “Schadenswert” aufweisen. Das kann daran liegen, dass am häufigsten das Thema “Corona” genannt wurde, wo häufig zwar ein Schaden thematisiert wird, aber eher ein geringer. (Kreuztabellen sind schwer zu texten!)

7.6.1 Nachrichtenwert und Resonanz mehrerer Medien

Mit dieser Analyse wird die Bedeutung der Nachrichtenfaktoren für die Selektion durch verschiedene Medien untersucht. Der Grundgedanke baut darauf auf, dass Ereignisse mit einem sehr hohen Nachrichtenwert im Grunde in allen Medien aufgegriffen werden. Wir untersuchen hier also, ob über die thematisierten Ereignisse in wenigen oder vielen Medien berichtet wurde. Dazu fassen wir die kodierten Themen pro Tag zusammen und schauen, in wie vielen Medien sie aufgegriffen wurden.

SELEKT <- DATEN_IA |> 
  group_by(TC, TAG, MEDIUM) |> # Dieser Schritt ist notwendig, damit Merhfachthematisierungen eines Ereignisses pro Tag in einem Medium nur jeweils einmal gezählt werden
  summarise(n = n(), # Anzahl der Themen pro Tag in einem Medium
            PERS_m = max(PERS), # Hier werden die höchsten Werte je NF genommen, die an einem Tag in einem Medium zu jedem Thema gefunden wurden
            KNTR_m = max(KNTR), 
            SCHAD_m = max(SCHAD),
            NAEHE_m = max(NAEHE)) |> 
  group_by(TC,TAG) |> # Jetzt kann auf Tag aggregiert werden, weil oben jedes Thema pro Tag und Medium gezählt wurde
  summarise(SELEKT = n(), # Anzahl der Medien, die die jeweiligen Themen aufgegriffen haben
            Personalisierung = max(PERS_m), # Hier wird das Maximum des jeweiligen NF genommen, also das Maximum der kodierten NF-Stärke aller Medien
            Kontroverse = max(KNTR_m),
            Schaden = max(SCHAD_m),
            Nähe = max(NAEHE_m)) |> 
  mutate(across(everything(), ~replace(.x, is.na(.x), 0))) |> 
  ungroup()

SELEKT |> 
  select(SELEKT:Nähe) |> 
  cor() |> # Hier wird wieder eine Tabelle mit kable produziert
    kableExtra::kable(caption = "Korrelationen zwischen NFs", digits = 2,
        booktabs = T, 
        align = c('rrrrr'), # die 5 steht für 5 Variablen
        linesep = "", # ohne diese Zeile, macht knitr alle 5 Zeilen einen kleinen Abstand, der oft kaum Sinn macht
      ##  col.names = c("Anstellung", "Lokal", "Regional", "National", "Transnational", "Gesamt"), # Damit können die Überschriften neu gemacht werden
        ) |>  # noch mehr Anpassungsmöglichkeiten für kable finden Sie bei google: r kable 
      kableExtra::kable_styling() |>  # hier können Sie stylen, aber bleiben Sie seriös :-)
  kableExtra::footnote(general = "Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.",
            general_title = "", # damit Kable unten nicht "Note" schreibt
            threeparttable = T # damit längere Fussnoten umgebrochen werden
           )

Korrelationen zwischen NFs
	SELEKT	Personalisierung	Kontroverse	Schaden	Nähe
SELEKT	1.00	0.38	0.32	0.32	0.35
Personalisierung	0.38	1.00	0.20	0.23	0.27
Kontroverse	0.32	0.20	1.00	0.39	0.21
Schaden	0.32	0.23	0.39	1.00	0.31
Nähe	0.35	0.27	0.21	0.31	1.00
Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.

Textbeispiel: Untersucht man, wie stark die Nachrichtenfaktoren die Selektion der Themen über die Medien hinweg steuern, können relativ starke Korrelationen festgestellt werden. Die Korrelationen zwischen der Personalsierung und der Auswahl durch mehrere Medien ist mit .38 am stärksten.

Alternativ und vielleicht schöner kann das in einem Korrelationsplot dargestellt werden:

Corr_SELEKT <- SELEKT |> 
  select(SELEKT:Nähe) |> 
  cor()

Corr_SELEKT_test <- SELEKT |> 
  select(SELEKT:Nähe) |> 
  corrplot::cor.mtest(conf.level = .95)

corrplot::corrplot(Corr_SELEKT, p.mat = Corr_SELEKT_test$p, 
         type = "lower", method = "square",
         addCoef.col = 'black',
         insig = "pch", diag = FALSE ,
         tl.cex=0.8, pch.cex = 0.8, tl.srt = 30)

rm(Corr_SELEKT, Corr_SELEKT_test)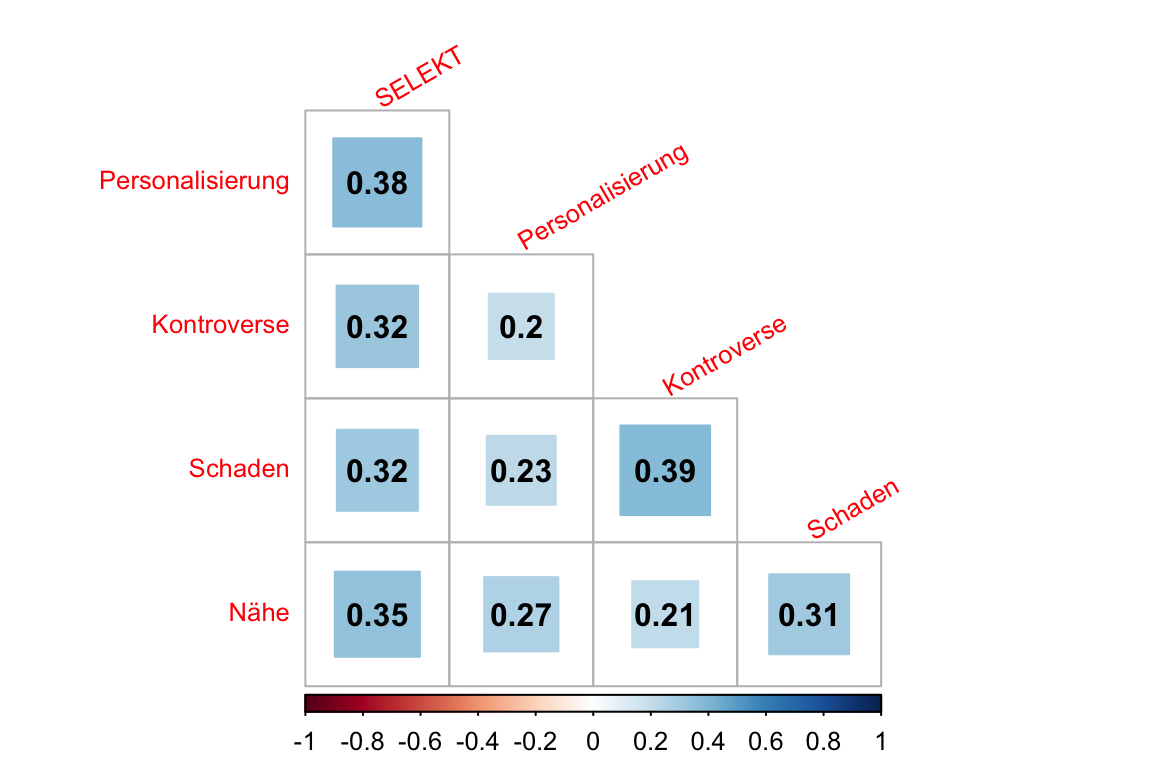

Korrelation der NFs mit der Anzahl der Medien, die über die Themen berichtet haben

Textbeispiel: (wie oben mit Fokus auf die erste Spalte mit der Selektion)

7.7 Thematisierung in Medien und Publikumsresonanz

Wenn Sie eine Hypothese zum Zusammenhang zwischen der Häufigkeit eines Themas in den Medien und der Häufigkeit der Nennungen durch das Publikum haben oder zwischen der Stärke eines NF in der Berichterstattung und den Nennungen durch das Publikum, dann müssen Sie die Daten zunächst aggregieren, weil Ihre Analyseeinheit grösser ist als Ihre Kodiereinheit (CE). Das kommt daher, dass Sie nicht Eigenschaften von Beiträgen in Beziehung setzen wollen, sondern die Anzahl von Beiträgen der jeweiligen Themen in Verbindung setzen wollen mit den Nennungen des Publikums. Die Anzahl der Beiträge muss daher eine Aggregationsstufe über den Artikeln liegen.

7.8 Zusammenspiel der Nachrichtenfaktoren

Das Zusammenspiel der Nachrichtenfaktoren lässt sich als Kreuztabellen oder als Korrelationen darstellen. Wenn sehr wenige Nachrichtenfaktoren verglichen werden sollen, geben die Kreuztabellen einen differenzierteren Einblick. Bei mehreren NFs ist es deutlich effizienter die Stärke der Zusammenhänge über Korrelationen abzubilden.


Corr_NF <- DATEN_IA |> 
  select(PERS:NAEHE) |> 
  as.matrix() |> 
  cor()

Corr_NF_test <- DATEN_IA |> 
  select(PERS:NAEHE) |> 
  corrplot::cor.mtest(conf.level = .95)

# mehr zu den corrplots hier: https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html
corrplot::corrplot(Corr_NF, p.mat = Corr_NF_test$p, 
         type = "lower", method = "square",
         insig = "pch", diag = FALSE ,
         tl.cex=0.6, pch.cex = 0.8, tl.srt = 45)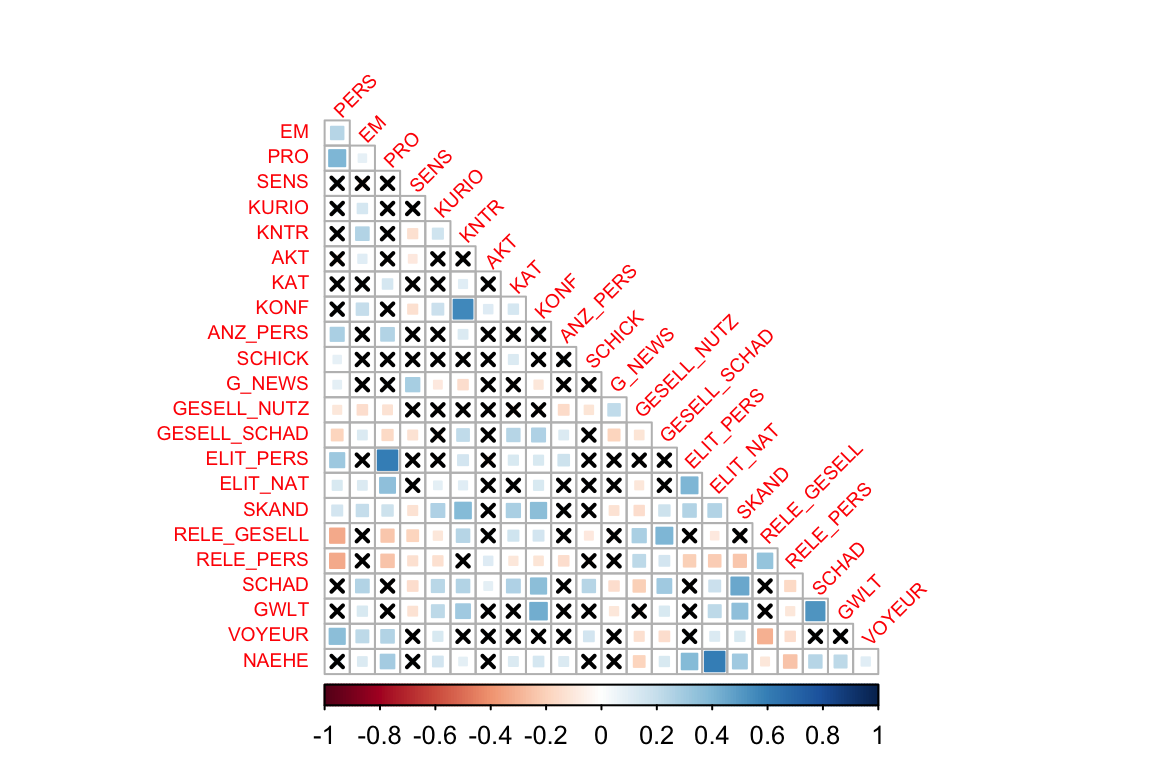

Textbeispiel: An den Korrelationen ist gut zu erkennen, dass manche Nachrichtenfaktoren eher zusammen auftreten, manche sich eher widersprechen und viele unabhängig voneinander sind (“x” im Feld für fehlende Signifikanz). Eine starke positive Korrellation findet sich zwischen “Elite-Personen” (ELIT_PERS) und “Prominenz” (PRO). Das ist sehr plausibel, weil Elitepersonen oft auch prominent sind. Auf der anderen Seite gibt es eine relativ starke negative Korrelation zwischen “gesellschaftlicher Relevanz” (RELE_GESELL) und “Personalisierung” (PERS). Themen mit gesellschaftlicher Relevanz sind also oft nicht personengebunden sondern von allgemeinerer und damit auch abstrakterer Natur.

7.8.1 Netzwerkplot der Korrelationen

Es gibt auch die Möglichkeit, die Nachrichtenfaktoren in so einem Netzwerkdiagramm darzustellen. Damit kann man sehen, welche Nachrichtenfaktoren stärker zusammenhängen (nahe beieinander) und welche eher unabhängig sind (weiter voneinander entfernt).

Corr_NF <- DATEN_IA |> 
  select(RELE_GESELL, RELE_PERS, PRO, PERS, KNTR, KONF, GESELL_SCHAD, GWLT, SCHAD) |> 
  corrr::correlate(diagonal = NA, quiet = TRUE) # oder 1, wenn Sie lieber die 1er in der Diagonalen haben 

Corr_NF |> 
  corrr::network_plot() # mehr zur Formatierung der network-plots erfahren Sie hier: https://corrr.tidymodels.org/reference/network_plot.html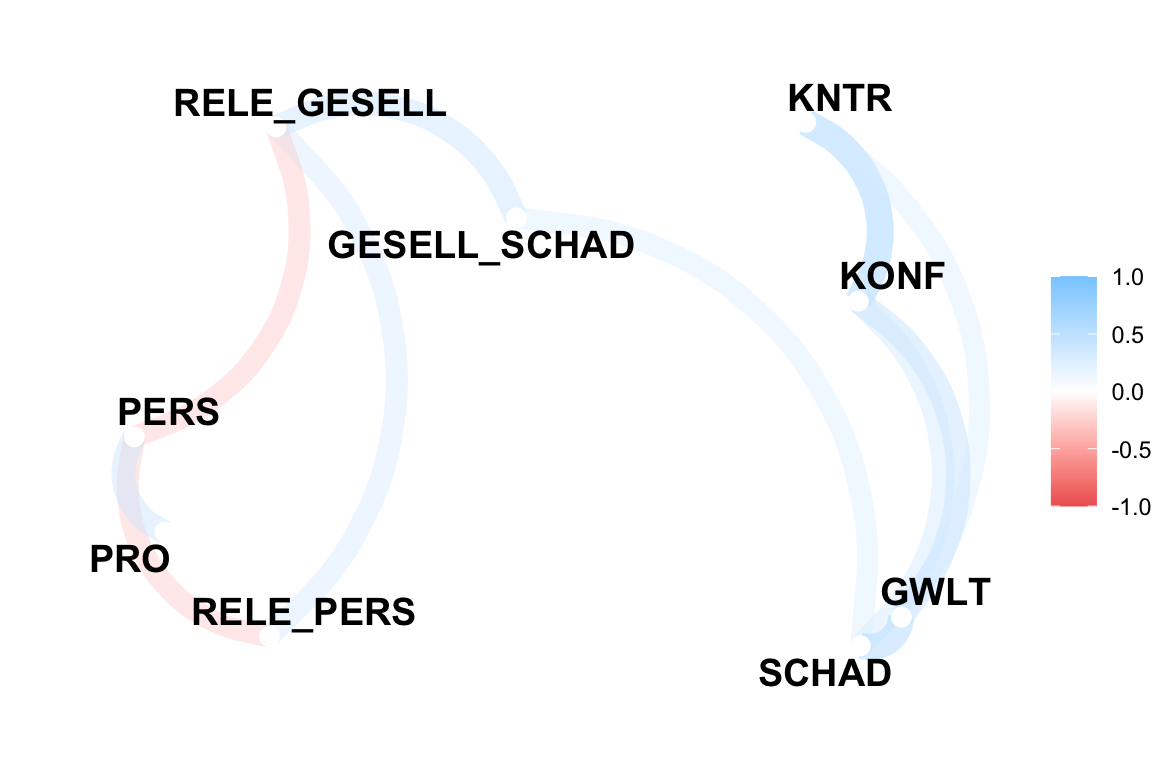

Die näher beieinanderliegenden Nachrichtenfaktoren hängen stärker miteinander zusammen als die stärker entfernten. In diesem Netzwerkdiagramm ist gut zu erkennen, dass “Kontroverse” (KNTR), “Konflikt” (KONF), “Gewalt” (GWLT) und “Schaden” (SCHAD) stärker miteinander zusammenhängen als mit “Personalisierung” (PERS) oder “gesellschaftlicher Relevanz” (RELE_GESELL). Auf der anderen Seite gibt es eine relativ starke negative Korrelation zwischen “gesellschaftlicher Relevanz” (RELE_GESELL) und “Personalisierung” (PERS).

7.9 Wirkung der NF auf die Beachtungsindikatoren

# # Wer noch mehr Kontrolle über die Tabelle möchte, kann das hier auskommentieren und sich mit lm.beta, tidy und kable austoben
Beacht_Rez_1_std <- lm.beta::lm.beta(Beacht_Rez_1)
# 
broom::tidy(Beacht_Rez_1_std) |>
  select(-estimate, -std.error) |>
kableExtra::kable(caption = "Regression auf Beachtung der Rezipienten", digits = 2,
        booktabs = T,
        align = c('lrrrrrrrrr'), # die 5 steht für 5 Variablen
        col.names = c("UVs",  "BETAs", "t", "p"),
        linesep = "", # ohne diese Zeile, macht knitr alle 5 Zeilen einen kleinen Abstand, der oft kaum Sinn macht
      ##  col.names = c("Anstellung", "Lokal", "Regional", "National", "Transnational", "Gesamt"), # Damit können die Überschriften neu gemacht werden
        ) |>  # noch mehr Anpassungsmöglichkeiten für kable finden Sie bei google: r kable
      kableExtra::kable_styling() |>  # hier können Sie stylen, aber bleiben Sie seriös :-)
  kableExtra::footnote(general = "Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.",
            general_title = "", # damit Kable unten nicht "Note" schreibt
            threeparttable = T # damit längere Fussnoten umgebrochen werden
           )

Regression auf Beachtung der Rezipienten
UVs	BETAs	t	p
(Intercept)	NA	14.03	0.00
PERS	-0.07	-1.58	0.12
KNTR	0.01	0.27	0.79
GESELL_SCHAD	0.22	4.82	0.00
Hier könnten/sollten Sie einen allgemeinen Hinweis oder eine kleine Erläuterung zur Tabelle geben.

Eine weitere Alternative ist jtools. Damit werden recht umfangreich Informationen über die Modelle inline in R-Studio ausgegeben und passabel im PDF rausgelassen. Nachteil ist die mässige bzw. umständliche Anpassbarkeit.

Observations	499
Dependent variable	Nenn_Gesamt
Type	OLS linear regression

F(3,495)	10.57
R²	0.06
Adj. R²	0.05

	Est.	2.5%	97.5%	t val.	p	VIF
(Intercept)	0.00	-0.09	0.09	0.00	1.00	NA
PERS	-0.07	-0.16	0.02	-1.58	0.12	1.05
KNTR	0.01	-0.08	0.10	0.27	0.79	1.06
GESELL_SCHAD	0.22	0.13	0.31	4.82	0.00	1.10
Standard errors: OLS; Continuous variables are mean-centered and scaled by 1 s.d.

Mehr dazu finden Sie hier.

apaTables::apa.reg.table(Beacht_Rez_1)
## 
## 
## Regression results using Nenn_Gesamt as the criterion
##  
## 
##     Predictor       b       b_95%_CI  beta   beta_95%_CI sr2  sr2_95%_CI     r
##   (Intercept) 18.67** [16.06, 21.29]                                          
##          PERS   -1.33  [-2.98, 0.33] -0.07 [-0.16, 0.02] .00 [-.01, .02] -.11*
##          KNTR    0.25  [-1.61, 2.12]  0.01 [-0.08, 0.10] .00 [-.00, .00]   .06
##  GESELL_SCHAD  7.50**  [4.45, 10.56]  0.22  [0.13, 0.31] .04  [.01, .08] .24**
##                                                                               
##                                                                               
##                                                                               
##              Fit
##                 
##                 
##                 
##                 
##      R2 = .060**
##  95% CI[.02,.10]
##                 
## 
## Note. A significant b-weight indicates the beta-weight and semi-partial correlation are also significant.
## b represents unstandardized regression weights. beta indicates the standardized regression weights. 
## sr2 represents the semi-partial correlation squared. r represents the zero-order correlation.
## Square brackets are used to enclose the lower and upper limits of a confidence interval.
## * indicates p < .05. ** indicates p < .01.
##

7.10 Test der Voraussetzungen linearer Modelle

Spätestens nach Ihren ersten Regressionsanalysen muss man natürlich auch mal checken, ob die Voraussetzungen überhaupt erfüllt sind. Das geht so:

# Balkendiagramm für Journalistische Beachtung
DATEN_IA |>
 count(Jour_Beacht) |> 
  ggplot(aes(x=Jour_Beacht, y=n)) +
  geom_bar(stat="identity")

# Die Verteilung Werte um die Regressionsgerade angucken

model.diag.metrics <- broom::augment(Beacht_Jour_1)

ggplot(model.diag.metrics, aes(PERS, Jour_Beacht)) +
  geom_point() +
  stat_smooth(method = lm, se = FALSE) +
  geom_segment(aes(xend = PERS, yend = .fitted), color = "red", size = 0.3)
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## `geom_smooth()` using formula = 'y ~ x'

ggplot(model.diag.metrics, aes(KNTR, Jour_Beacht)) +
  geom_point() +
  stat_smooth(method = lm, se = FALSE) +
  geom_segment(aes(xend = KNTR, yend = .fitted), color = "red", size = 0.3)
## `geom_smooth()` using formula = 'y ~ x'

# VarianzInflationsFaktor und Tolerance anschauen
olsrr::ols_vif_tol(Beacht_Jour_1)
##      Variables Tolerance      VIF
## 1         PERS 0.9552986 1.046793
## 2         KNTR 0.9421957 1.061351
## 3 GESELL_SCHAD 0.9128623 1.095455
  
# Residuen visuell checken (Homoskedastizität)
plot(Beacht_Jour_1)

# Wenn der Breusch–Pagan Test signifikant wird, dann liegt Heteroskedastizität vor
lmtest::bptest(Beacht_Jour_1)
## 
##  studentized Breusch-Pagan test
## 
## data:  Beacht_Jour_1
## BP = 20.051, df = 3, p-value = 0.0001656

# Histogramm der Residuen (check der Normalverteilung)
hist(Beacht_Jour_1$residuals)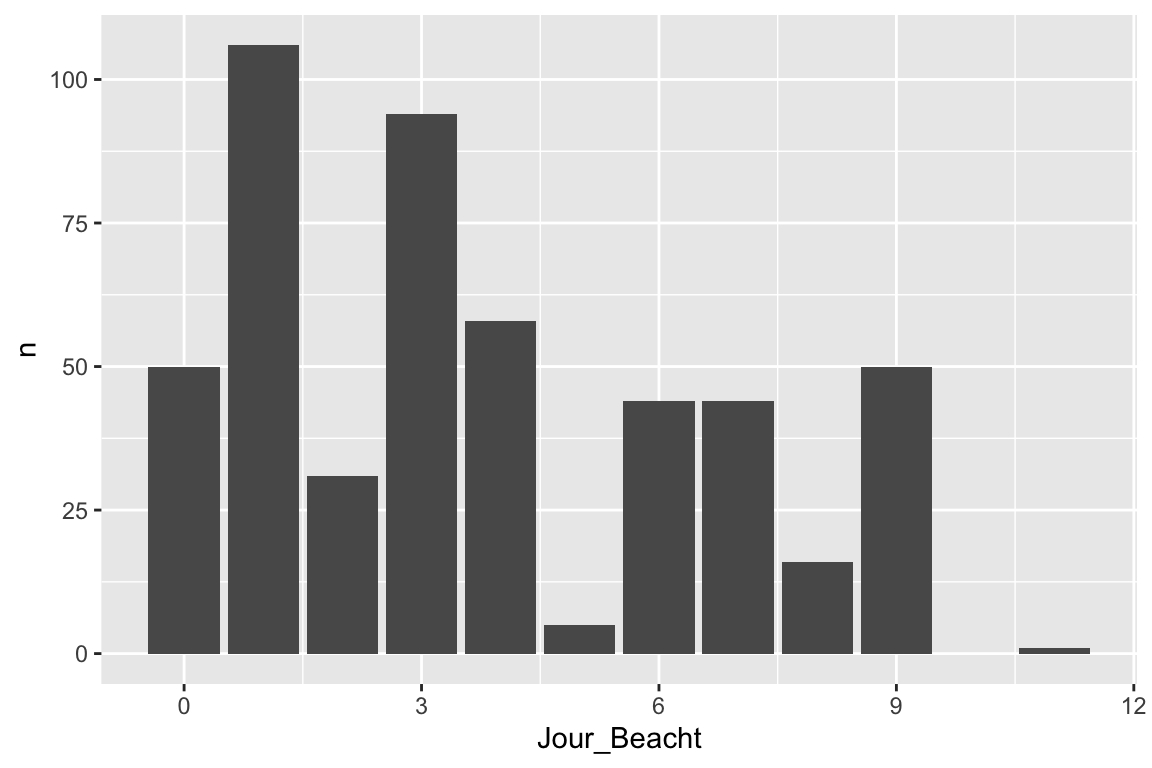

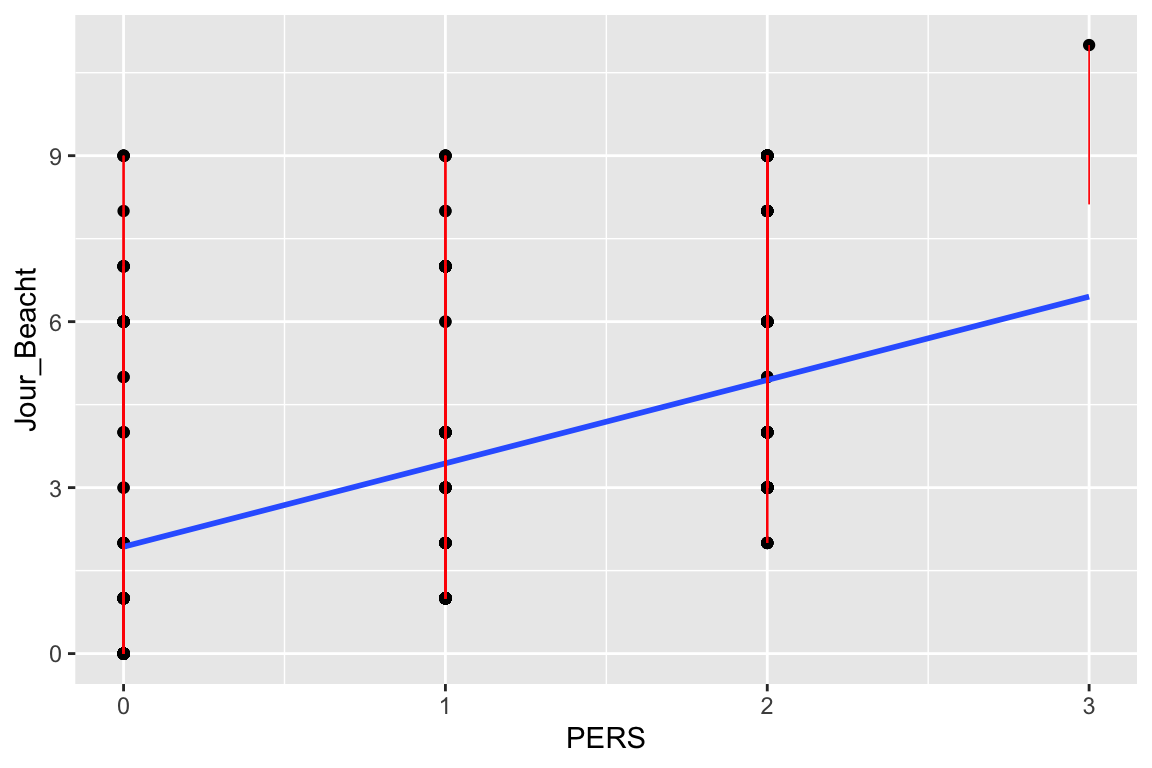
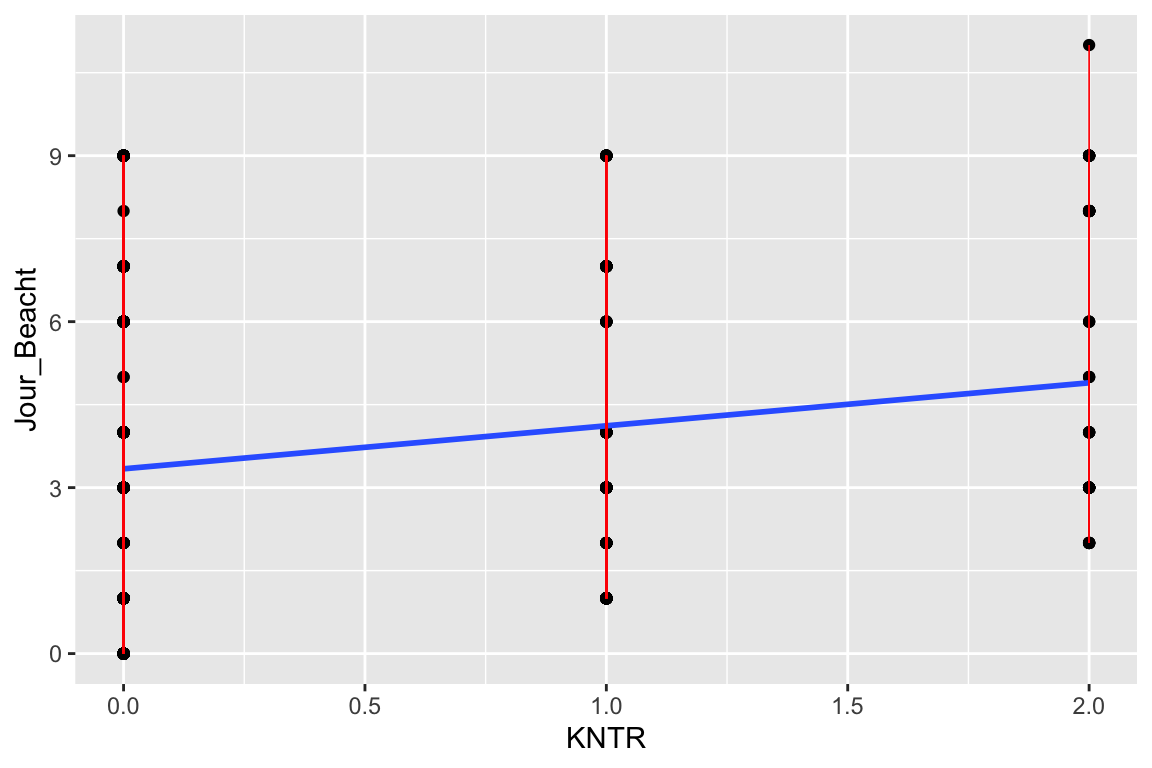
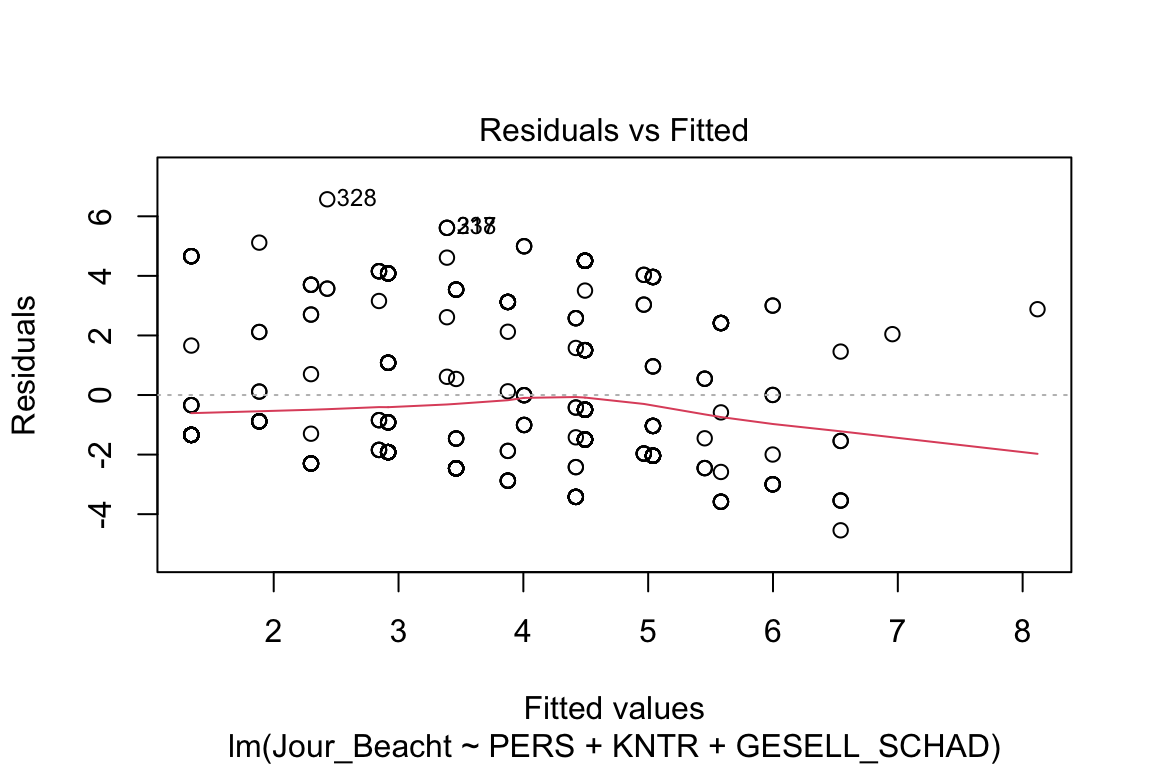
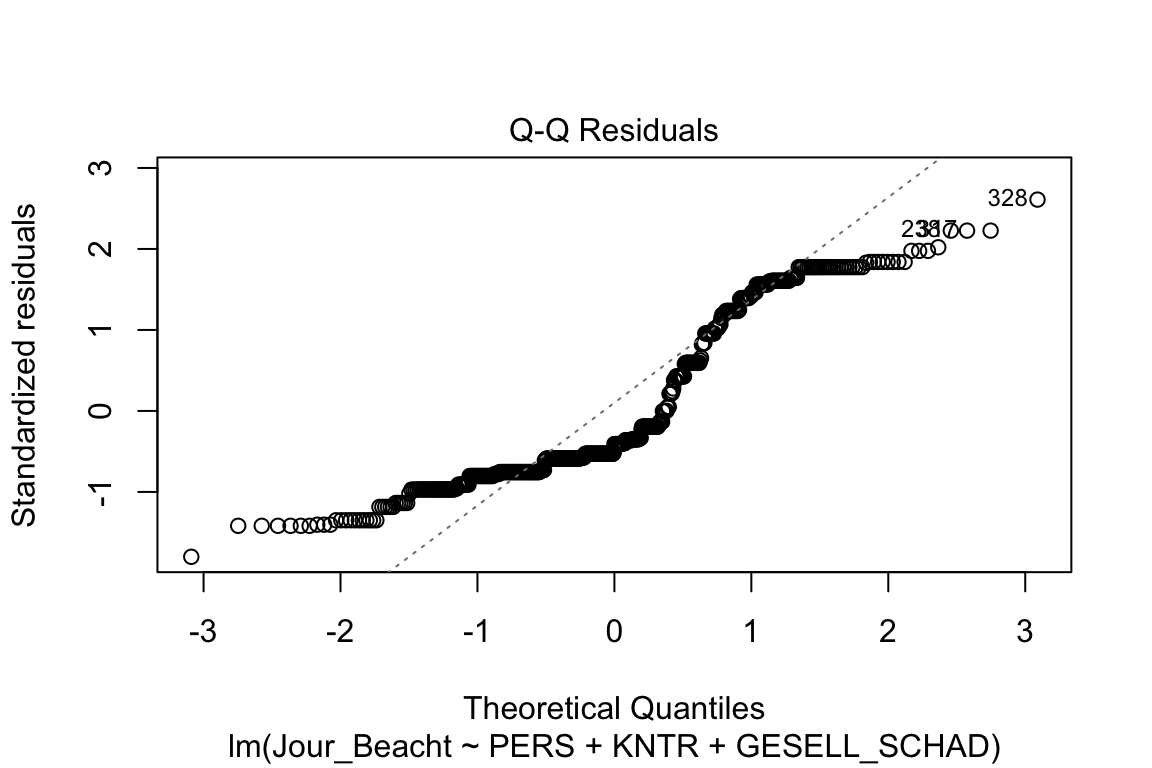
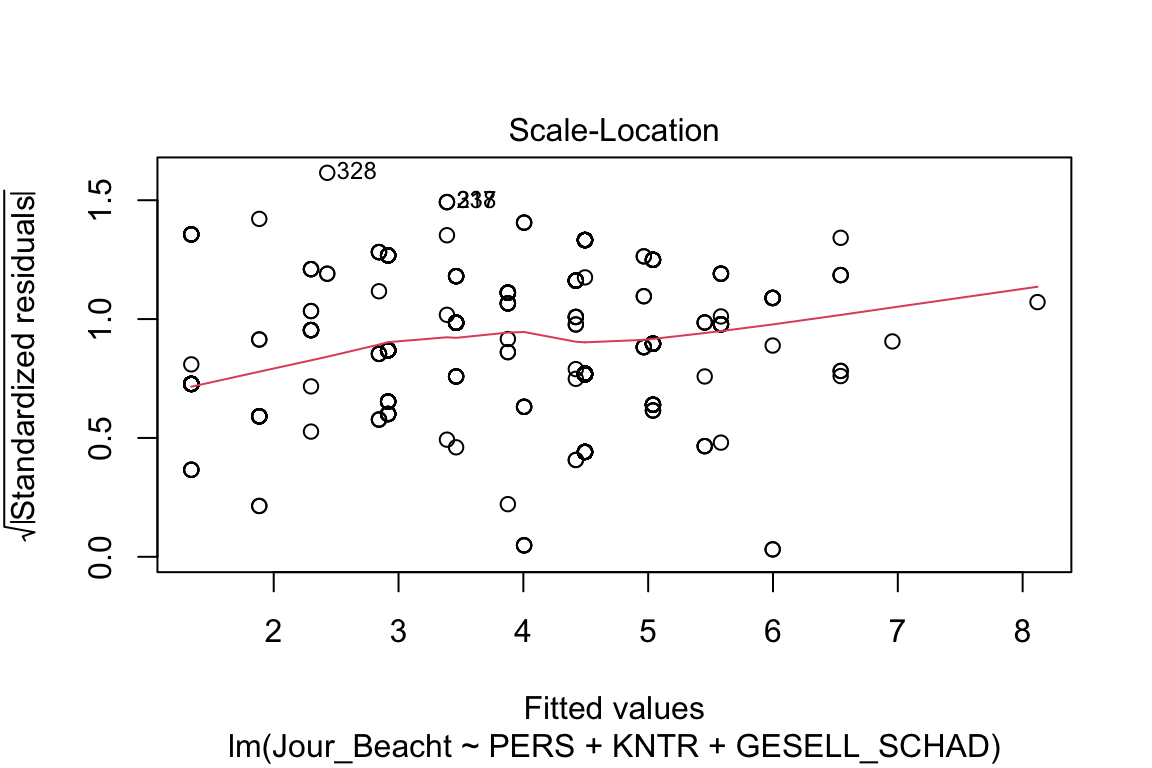
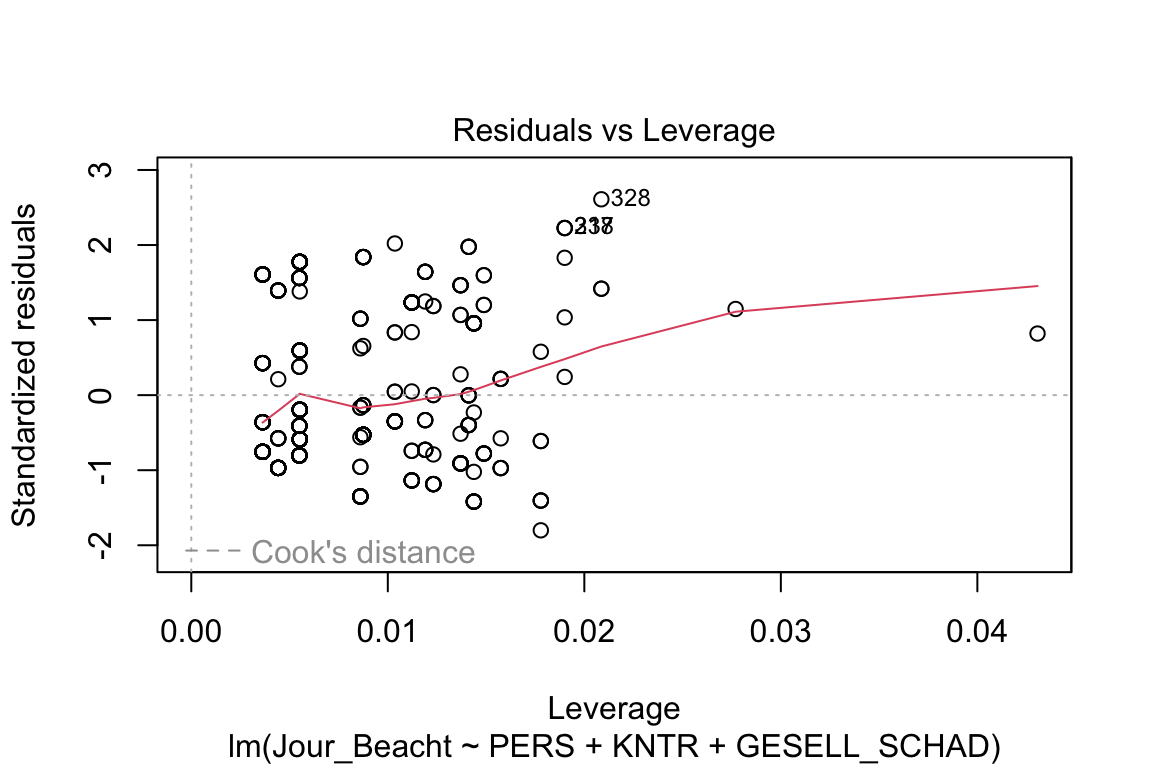
Diese ganzen Grafiken gehören eher in den Anhang und nicht so sehr in den Haupttext. Bei Verletzungen überlegen Sie, was Sie tun könnten und wenn Sie die Lösungen noch nicht gelernt haben, dann überinterpretieren Sie knappe Hypothesenentscheidungen besser nicht.

7.10.1 Regressionsdiagramm (Whyskerplot)

Tabellen sind einigermassen informativ. Besser lesbar ist allerdings die folgende Darstellung mit einem Whiskerplot, die auch sehr gut im PDF funktioniert, weil es eine Abbildung ist!

# mehr zu plot_models hier: https://strengejacke.github.io/sjPlot/articles/plot_model_estimates.html
sjPlot::plot_models(Beacht_Rez_1, Beacht_Jour_1, 
            std.est = "std", # Für die (vergleichbaren) standardisierten Regressionskoeffizienten
            title = "NFs und Beachtung",
            legend.title = "Beachtung",
            show.values = TRUE) +
  ylim(-.5, .8) # von wo bis wo die X-Achse geht, wenn sehr viel leere Fläche da ist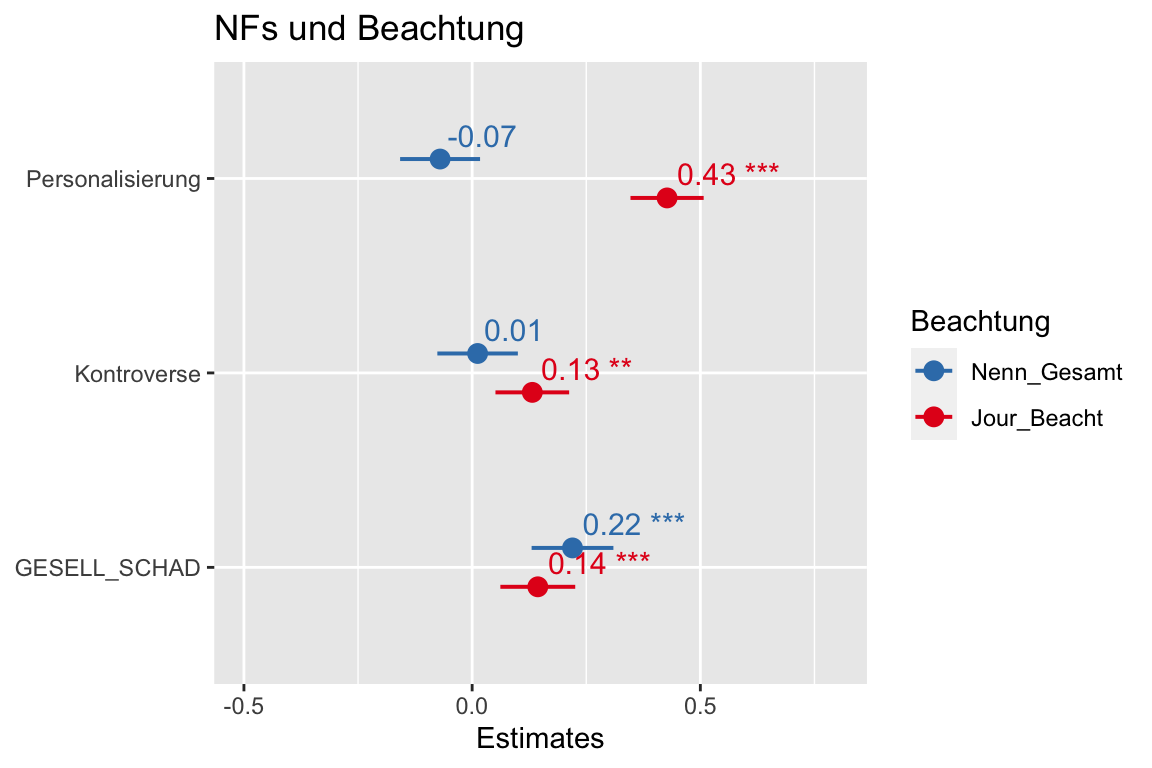

Textbeispiel: “Personalisierung” wirkt auf die Beachtung durch Rezipipenten nur minimal und eher negativ (-.06). Insgesamt nennen die Befragten also etwas seltener Meldungen, wo die Personalisierung hohe Werte hat. Allerdings liegt 0 im Konfidenzintervall dieses kleinen Effekts; er ist also nicht signifikant. Im Unterschied dazu besteht ein starker positiver Zusammenhang zwischen der Personalisierung und der journalistischen Beachtung (.36). Personalisierung ist also ein stark journalistischer Nachrichtenfaktor.

Der Nachrichtenfaktor “Kontroverse” zeigt kleine positive Zusammenhäng mit der Beachtung durch die Rezipienten (.04) und mit der journalistischen Beachtung (.09). Allerdings ist die Wirkung auf die Rezipientenerinnerung nicht signifikant. Das Gewicht des Nachrichtenfaktors “Kontorverse” in Bezug auf die journalistische Beachtung ist signifikant von 0 verschieden.

7.11 Vergleich der NF-Gewichte nach Mediengruppen

Hier werden die NF-Gewichte nach Mediengruppe verglichen.

# mehr zu plot_models hier: https://strengejacke.github.io/sjPlot/articles/plot_model_estimates.html

# wichtig hier am Ende der Zeile, wo das subset festgelegt wird (hier Medium_Q == 1 für Qualitätsmedien)
Beacht_Quali_1 <- lm(Nenn_Gesamt ~ PERS + KNTR + GESELL_SCHAD + Population, subset(DATEN_IA, Medium_Q == 1))

# wichtig hier am Ende der Zeile, wo das subset festgelegt wird (hier Medium_Q == 2 für Boulevardmedien)
Beacht_Boulevard_1 <- lm(Nenn_Gesamt ~ PERS + KNTR + GESELL_SCHAD + Population, subset(DATEN_IA, Medium_Q == 2))

sjPlot::plot_models(Beacht_Rez_1, Beacht_Quali_1, Beacht_Boulevard_1, 
            std.est = "std", # Für die (vergleichbaren) standardisierten Regressionskoeffizienten
            title = "Gewichte der NFs nach Medientypen",
            legend.title = "Beachtung",
            m.labels = c("Gesamt", "Qualitätsmedien", "Boulevard"),
            axis.title = "Regressionsgewichte",
            show.values = FALSE) +
  ylim(-.25, .6) # wenn was fehlt in auskommentieren und schauen von wo bis wo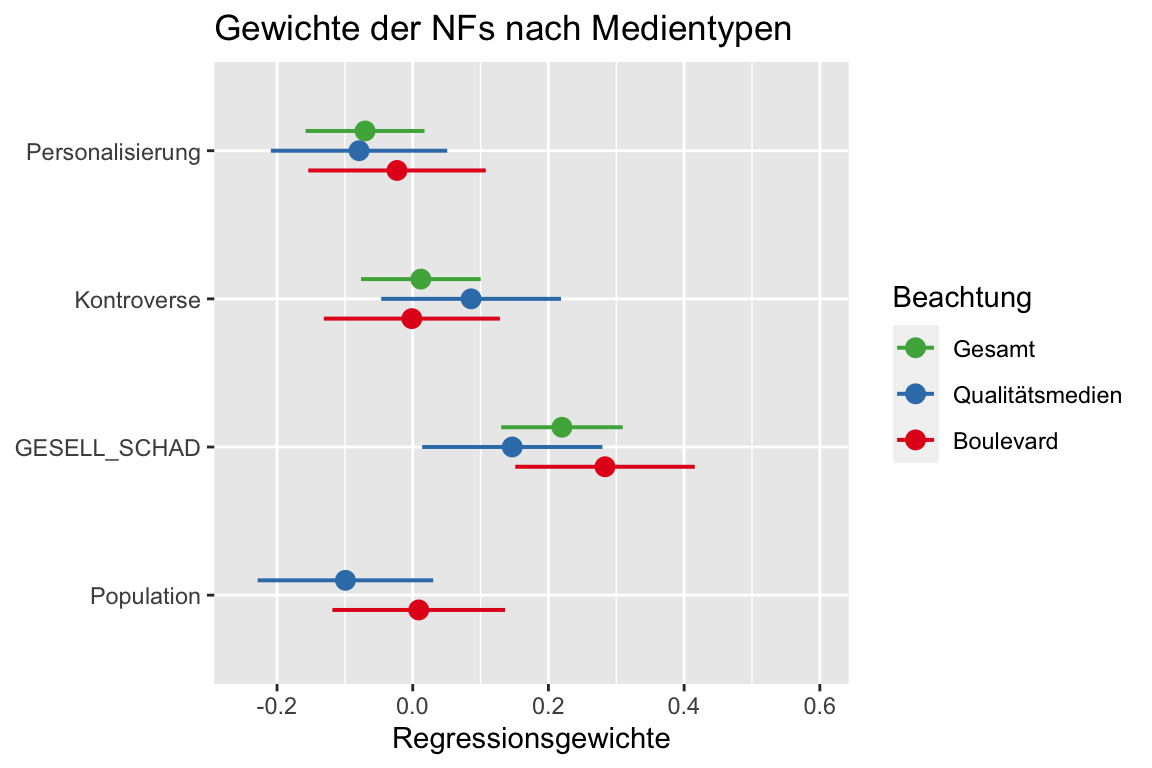

7.12 Unterschiede der Gewichte von NF nach Befragtenmerkmalen

Zu diesen Auswertungen und den Voraussetzungen in der Datenaufbereitung habe ich noch ein Video erstellt:

7.12.1 Zwei Gruppen als UV

Sie können Unterschiede in der Bedeutung (Gewicht) der Nachrichtenfaktoren mit eine Unterschiedstest untersuchen. Dazu müssen Sie die NF aus der Inhaltsanalyse an die Befragung matchen (siehe @ref(IAanBefragung)). Für diese Analyse brauchen Sie die fusionierten Daten und die Variablen GESCHL für Geschlecht und KNTR_m für die durchschnittlichen Kontroversewerte der genannten Meldungen.

DATEN_BF_IA <- readRDS("data/Befragung_und_IA.RDS") |>
  mutate(GESCHL = S201, 
          Alter = 2023 - as.numeric(S204_01)) |>
    mutate(ALTER_gr = case_when(
    Alter < 0 ~ NA_real_,
    Alter <= 25 ~ 1,
    Alter <= 45 ~ 2,
    Alter <= 65 ~ 3,
    Alter <= 85 ~ 4,
    Alter > 85 ~ 5
  )) |>
  rowwise()|>
  mutate(KNTR_m = sum(c(KNTR_1, KNTR_2, KNTR), na.rm = TRUE))|>
  ungroup()

Jetzt kann ein t-test gerechnet werden. Dann kann dieser t-test auch in einem Diagramm der Mittelwerte mit den Konfidenzintervallen als Annotation verwendet werden:

t_test <- DATEN_BF_IA |>
  filter(GESCHL < 3) |>
   t.test(KNTR_m ~ GESCHL, data = _) # t-Test ausführen und in t_test schreiben

t_Wert <- round(t_test$statistic,2)
p_Wert <- round(t_test$p.value, 3)
df <- round(t_test$parameter,0)

### Hier werden die Werte aus dem t-Test in einen Text geschrieben, den Sie in einer Grafike als Annotation verwenden können
t_Test_Geschlecht_KNTR = paste0("t-Test: \n",
  "p-Wert = ", p_Wert, # den p-Wert aus der t_test-List-Ausgabe
       "\n (t = ", t_Wert,  # den T-Wert (statistic) aus der t_test-List-Ausgabe
       ", df = ", df, ")") # und die df (parameter) aus der t_test-List-Ausgabe

df.summary <- DATEN_BF_IA   %>%  ## Daten der Befragung mit Ihren angehängten NF
  filter(GESCHL < 3) |>
  select(GESCHL, KNTR_m) |>
  group_by(GESCHL) |>
  summarise(
    ci_d = 1.96*sd(KNTR_m, na.rm = TRUE)/sqrt(n()),
    KNTR_m = mean(KNTR_m, na.rm = TRUE))

df.summary |>
  mutate(GESCHL = case_match(GESCHL,
    1 ~ "weiblich", 
    2 ~ "männlich"
  )) |>
  ggplot(aes(x = GESCHL, y = KNTR_m, ymin = KNTR_m-ci_d, ymax = KNTR_m+ci_d, color = GESCHL)) +
  geom_errorbar(width = 0.2) +
  geom_point(size = 1.5) +
    labs(x = "Geschlecht", y = "KNTR_m",
       title = "Bedeutung des NF Tierbezug nach Geschlecht",
       subtitle = "Mittelwertvergleich mit Konfidenzintervall") +
  theme(legend.position = "none") +
  annotate("text", x = Inf, y = 1, label = t_Test_Geschlecht_KNTR, vjust = -1, hjust = 1) +
  theme_minimal()

rm(t_Wert, p_Wert, df)
rm(t_Test_Geschlecht_KNTR)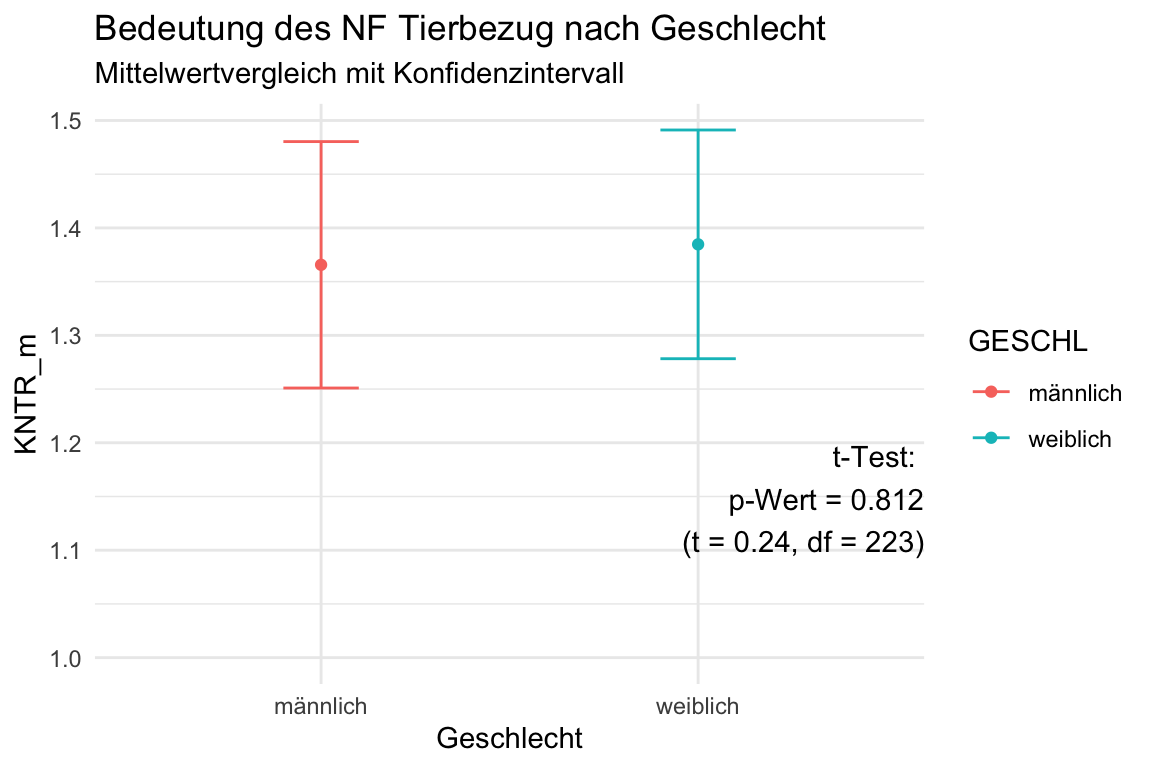

7.12.2 Mehrere Gruppen als UV

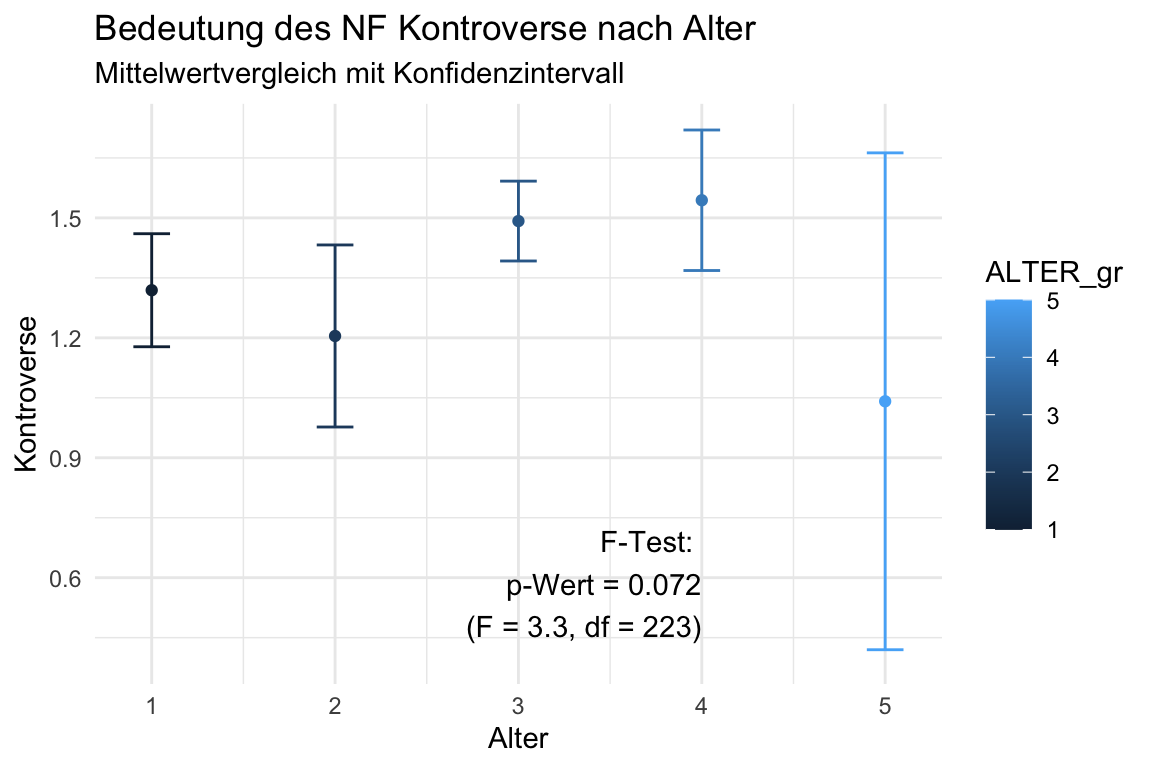
Hier werden die Mittelwerte für den Nachrichtenfaktor KNTR (Kontroverse) nach Altersgruppen verglichen (gebaut wurde KNTR_m in der Datenaufbereitung siehe @ref(IAanBefragung)). Sie können schauen, ob die Mittelwerte sich zwischen den Gruppen unterscheiden, wenn Sie die Konfidenzintervalle (KI) anschauen. Wenn die KIs sich nicht überschneiden, dann sind die Unterschiede signifikant.

# Erstmal eine ANalysis Of VAriance = ANOVA für die Variable KNTR_m nach Altersgruppen (Alter)
ANOVA <- aov(KNTR_m ~ ALTER_gr, data = DATEN_BF_IA)

# summary(ANOVA)
p_Wert <- round(summary(ANOVA)[[1]][1,5],3) # hier wird der p-Wert aus der Summary der ANOVA gespeichert
F_Wert <- round(summary(ANOVA)[[1]][1,4],1) # hier der F-Wert
df <- round(summary(ANOVA)[[1]][2,1],0) # hier die df

### Hier werden die Werte aus dem F-Test in einen Text geschrieben, den Sie in einer Grafike als Annotation verwenden können
ANOVA_Alter_KNTR = paste0("F-Test: \n",
  "p-Wert = ", p_Wert, # den p-Wert aus der t_test-List-Ausgabe
       "\n (F = ", F_Wert,  # den F-Wert (statistic) aus der t_test-List-Ausgabe
       ", df = ", df, ")") # und die df (parameter) aus der t_test-List-Ausgabe

df.summary <- DATEN_BF_IA   %>%  ## Daten der Befragung mit Ihren angehängten NF
  select(ALTER_gr, KNTR_m) |>
  group_by(ALTER_gr) |>
  summarise(
    ci_d = 1.96*sd(KNTR_m, na.rm = TRUE)/sqrt(n()),
    KNTR_m = mean(KNTR_m, na.rm = TRUE))

df.summary |>
  filter(!is.na(ALTER_gr))|>
  ggplot(aes(x = ALTER_gr, y = KNTR_m, ymin = KNTR_m-ci_d, ymax = KNTR_m+ci_d, color = ALTER_gr)) +
  geom_errorbar(width = 0.2) +
  geom_point(size = 1.5) +
    labs(x = "Alter", y = "Kontroverse",
       title = "Bedeutung des NF Kontroverse nach Alter",
       subtitle = "Mittelwertvergleich mit Konfidenzintervall") +
  theme(legend.position = "none") +
  annotate("text", x = 4, y = 0.4, label = ANOVA_Alter_KNTR, vjust = -.2, hjust = 1) +
  theme_minimal()

rm(F_Wert, p_Wert, df)
rm(ANOVA_Alter_KNTR)